Théorie des Graphes

Arbre :

Un arbre est un graphe connexe qui ne possède pas de cycle.

Propriétés/Théorèmes : Les Propriétés suivantes sont équivalentes (elles définissent des arbres) :

1. $G$ est connexe et sans cycle.
2. $G$ est connexe et $|R|=|N|-1$
3. $G$ est sans cycle et $|R|=|N|-1$
4. $G$ est sans cycle et lui ajouter une arête crée un et un seul cycle.
5. $G$ est connexe et supprimer une arête quelconque le déconnecte.
6. Deux nœuds distincts de $G$ sont reliés par un et un seul chemin (et $G$ est sans boucle)

Feuille :

Soit $G=(N,R)$ un arbre. On dit qu’un nœud $n\in N$ est une feuille de $G$ si $\text{deg}(n)=1$.

Propriétés/Théorèmes :

1. Les extrémités du chemin le plus long dans un arbre sont des feuilles de degré 1. Preuve : Soit $c=(n_1,n_2,\dots ,n_m)$ un chemin de longueur maximale dans $G$ (ce chemin n’est pas nécessairement unique, mais il en existe au moins un). On voit que $\text{deg}(n_1)\ge 1$ puisque $n_1$ est adjacent à $n_2$. Si $n_1$ était de degré strictement supérieur à $1$, il devrait exister un nœud $n$ adjacent à $n_1$ et distinct de $n_2$. Si $n$ se trouve sur le chemin défini plus haut, alors $G$ possède un cycle, ce qui contredit le fait que $G$ est un arbre. Si $n$ ne se trouve pas sur le chemin défini plus haut, alors $c$ peut être étendu en le préfixant par $n$, ce qui contredit l’hypothèse que $c$ est un chemin de longueur maximale. On en conclut que $\text{deg}(n_1)=1$. Le même raisonnement s’applique à $n_m$, et on a donc identifié deux nœuds de degré $1$.

Arbre sous-tendant

L’arbre $G^{\prime }=(N^{\prime },R^{\prime })$ est un arbre sous-tendant le graphe $G=(N,R)$ si $N=N^{\prime }$ et $R^{\prime }\subseteq R$

Propriétés/Théorèmes :

1. $G$ est connexe $\iff G$ possède un arbre sous-tendant

Arbre sous-tendant de poids minimum

$A$ est un arbre sous-tendant de poids minimum de $G$ ssi $A$ sous-tend $G$ et tout arbre $A^{\prime }$ sous-tendant $G$ est tel que $c(A)\le c(A^{\prime })$.

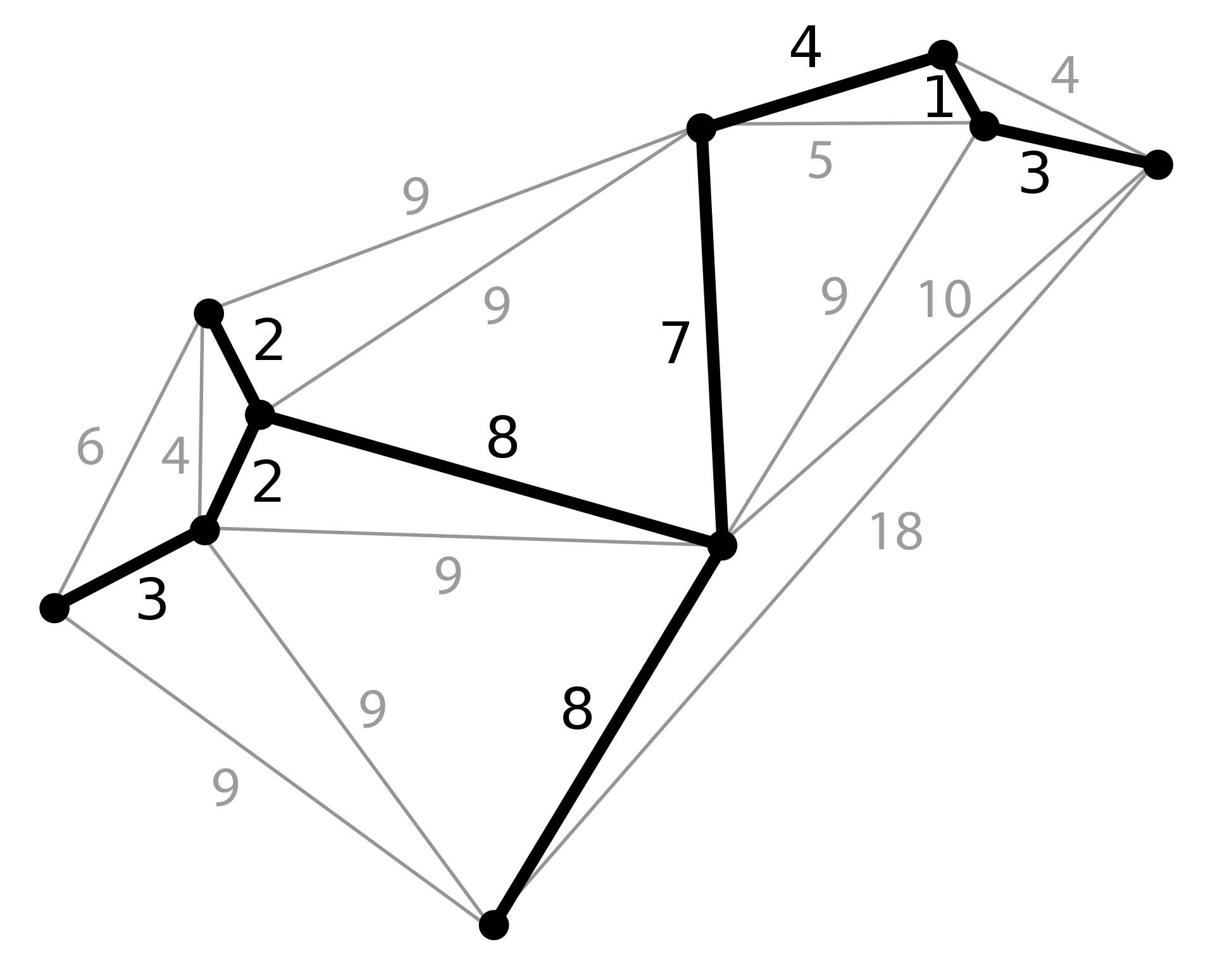
Exemple(s)