Intoduction

Très Illustres et très chevalresques champions, gentilshommes, IA autonomes et autres, bienvenue dans ce livre des interwebs qui reprend certains des éléments les plus notoires de la théorie des graphes.

Ce livre a été créé dans le but d'avoir un document de reference qui ne fait pas saigner des yeux, accessible de partout et facile d'utilisation pour la partie qui concerne la théorie des graphes du cours LEPL1108 à l'UCLouvain. Il contient également certains ajouts personnels que je trouve pertinents/interessants et qui ne sont pas vus dans le cours. Le but final est d'avoir un livre de référence le plus complet possible sur la théorie des graphes.

Donc si vous trouvez qu'un certain sujet devrait être inclus dans le libre, n'hésitez pas à contribuer au repositoire github de ce livre. Il ne faut pas s'y connaître en Rust/mdBook/développement web pour contribuer, il suffit d'avoir un éditeur markdown/Latex (je recommande Obsidian avec l'extension Latex Suite) et de savoir utiliser git.

Pour le moment le livre contien deux grand chapitres :

Bases et définitions : qui donne les bases de la théorie des graphes et définit les termes utiles de façon rigoureuse.
Algorithmes : qui présente les algorithmes les plus importants de la théorie des graphes, les explique, propose une implémentation et démontre qu'ils sont corrects.

Conseil(s) :

Si vous cherchez un terme spécifique utilisez la petite loupe en haut à gauche pour faire une recherche rapide

Bases et Définitions

Cette section reprend les définitions rigoureuses (enfin je l'espère) et propriétés qui forment la base de la théorie des graphes vue dans le cours LEPL1108 à l'UCLouvain.

Il est divisé en 4 chapitres :

Notions de Base :

Nœud/Sommet/Point :

Unité fondamentale d'un graphe

Propriétés/Théorèmes :

Deux sommets sont voisins s'ils sont reliés par une arête.
Deux sommets sont indépendants s'ils ne sont pas voisins.
Le degré d'un sommet est le nombre d'arêtes incidentes à ce sommet les boucles comptant double.

Graphe :

Un graphe est un triple $G = (N, R, I)$ :

$N :$ ensemble fini nœuds notés $(i, j, k, \dots)$
$R :$ ensemble fini d'arêtes notées ( $α, β, γ \dots$ )
$I :$ une relation d'incidence $\subset N \times R$ telle que toute arête est incidente à 1 ou 2 nœuds (cette relation est généralement sous-entendue pour un graphe donné)

Propriétés/Théorèmes :

Un graphe $G$ est dit d'ordre $n$ si $∣ N ∣ = n$

Arête/Lien/Ligne :

liaison entre deux sommets d'un graphe

Propriétés/Théorèmes :

Une arrête $α \in R$ est une boucle si $∣ {i ∣ (i, α) \in I} ∣= 1$ :
$(i, α) \in I$ : Indique que la paire $(i, α)$ est un élément de l'ensemble $I$ .
$i ∣ (i, α) \in I$ : Désigne l'ensemble des $i$ tels que $(i, α)$ ce trouve dans l'ensemble des relations d'incidence c'est à dire l'ensemble des connexions arête nœud.
$∣ {i ∣ (i, α) \in I} ∣$ Désigne la taille de l'ensemble susmentionné.

Notions Dérivées :

Parcours/Chaîne :

Un parcours $P$ de longueur $k$ dans $G$ est une suite alternée $P := (i_{0}, α_{1}, i_{1}, α_{2}, i_{2}, \dots, α_{k}, i_{k})$ de $k + 1$ nœuds et $k$ arêtes de $G$ .

Propriétés/Théorèmes :

Un parcours est dit fermé si $i_{0} = i_{k}$ et ouvert sinon.

Piste/Chaîne simple :

Une piste est un parcours dont les arêtes sont distinctes

Chemin/Chaîne élémentaire (Définition de chemin de LEPL1108)) :

Un chemin est un parcours ouvert dont tous les nœuds sont distincts.

Cycle/Circuit (Définition d'un cycle plus répandue dans la littérature et plus utile à mon avis) :

Un cycle est une suite d'arêtes consécutives distinctes (chaine simple) dont les deux sommets extrémités sont identiques.

Cycle (Définition donnée dans LEPL1108) :

Un parcours dont tous les nœuds et arêtes sont distincts, à l’exception du premier et du dernier nœud.

Isthme :

Considérons un graphe connexe $G = (N, R)$ . Une arête $α \in R$ est appelée un isthme de $G$ si la présence de $α$ est indispensable à la connexité, c’est-à-dire si le graphe partiel $G_{α}^{*} := (N, R ∖ {α})$ n’est pas connexe.

Graphe Simple :

Un graphe est simple si il n’a ni boucle ni nœuds reliés par des arêtes multiples. $α = {i, j}$ identifie alors l'unique arête telle que $(i, α) \in I$ et $(j, α) \in I$

Propriétés/Théorèmes :

Un graphe simple est biparti si et seulement s'il ne possède aucun cycle de longueur impaire (explication de la partie nécessaire de cette équivalence : Si on imagine un cycle de longueur 3, on place un nœud dans $U$ et dans $V$ , où place-t-on le troisième nœud ? Dans les 2 cas on aura une arête avec ses extrémités dans un même ensemble )
Un graphe simple non orienté d'ordre $n$ a au maximum $\frac{n ( n - 1 )}{2}$ arêtes

Graphe Connexe :

Un graphe est connexe si il existe un parcours reliant toute paire de nœuds.

Graphe Biparti :

Un graphe est dit biparti si son ensemble de sommets peut être divisé en deux sous-ensembles disjoints $U$ et $V$ tels que chaque arête ait une extrémité dans $U$ et l'autre dans $V$ .

Parcours/Chaine eulérien(ne) :

Un parcours qui passe par toutes les arêtes, une seule fois.

Propriétés/Théorèmes :

Un graphe connexe a un parcours eulérien si il possède 0 ou 2 arêtes de degré impair.

Cycle/Circuit/Tournée Eulérien(ne) :

Parcours eulérien qui revient au sommet/nœud de départ (ici on parle de cycle définit comme une chaîne simple/piste fermée).

Graphe Eulérien :

Graphe possédant au moins un cycle eulérien (ici on parle de cycle définit comme une chaîne simple/piste fermée).

Exemple(s) :

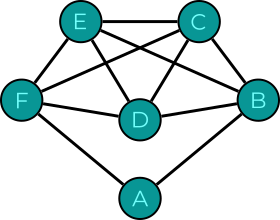
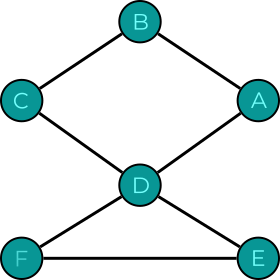
Propriétés/Théorèmes :

Un graphe connexe dont les nœuds sont tous de degré pair est un graphe eulérien et inversement.

Piste/Parcours/Chaîne Eulérien(ne) :

Piste qui passe par toutes les arêtes.

Propriétés/Théorèmes :

Le graphe $G$ sans nœud isolé possède une piste eulérienne si $G$ est sans nœud isolé est connexe et contient soit 0 soit 2 nœuds de degré impair.

Chemin Hamiltonien :

Un parcours passant par tous les nœuds du graphe une et une seule fois.

Cycle Hamiltonien :

Un cycle passant par tous les nœuds du graphe une et une seule fois.

Graphe Hamiltonien :

Graphe simple possédant un cycle hamiltonien.

Isomorphisme :

Les graphes simples $G = (N, R)$ et $G^{'} = (N^{'}, R^{'})$ sont isomorphes si :

Il existe une bijection $f : N \to N^{'}$
${i, j} \in R \Leftrightarrow {f (i), f (j)} \in R^{'}$

Propriétés/Théorèmes :

1 : La relation d'isomorphisme est une relation d'équivalence sur les graphes 2 : Il est facile de vérifier si $f$ définit un isomorphisme Il reste difficile de décider si deux graphes sont isomorphes

Matrice d'incidence :

La matrice d’incidence d’un graphe $G = (n, R)$ est la matrice de genre $∣ N ∣ \times ∣ R ∣$ dont chaque entrée $(i, α) \in N \times R$ vaut :

$2$ si l’arête $α$ est une boucle sur le nœud $i$ ,
$1$ si $α$ relie $i$ à un autre nœud,
$0$ si $α$ n’est pas incidente à i.

Exemple(s) :

Matrice d'Adjacence :

La matrice d’adjacence $A$ est de genre $∣ N ∣ \times ∣ N ∣$ :

$a_{i, j} :=$ nombre d’arêtes reliant $i$ et $j$ si $i \neq = j$
$a_{i, i} :=$ deux fois le nombre de boucles sur $i$

Exemple(s) :

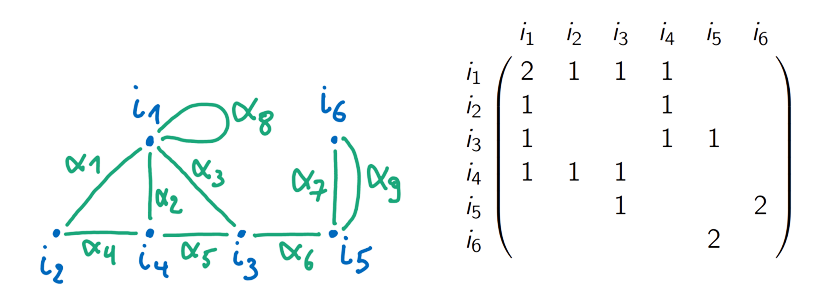
Propriétés/Théorèmes :

Soient 2 graphes $G_{1}$ et $G_{2}$ avec comme matrices d'adjacence $A_{1}$ et $A_{2}$ . $G_{1}$ et $G_{2}$ sont isomorphes si et seulement si il existe une matrice de permutation $P$ tel que : $P A_{1} P^{- 1} = A_{2}$ $A_{1}$ et $A_{2}$ sont donc semblables. Dit autrement: si on peut permuter les noms des nœuds de telle sorte que que $G_{1}$ devient $G_{2}$ alors les graphes sont isomorphes et la permutation des noms est équivalent à permuter les lignes et les colonnes de la matrice ce qui correspond à la formule ci-dessus.
$\sum_{j \in N} a_{i, j} = \sum_{j \in N} a_{j, i} = deg (i)$ La somme des termes sur une lignes ou une colonne correspond au degré du nœud associé à cette ligne/colonne.
$\sum_{(i, j) \in N^{2}} a_{i, j} = 2∣ R ∣$ La somme de tous les éléments de la matrice est égal au double du nombre d'arêtes dans le graphe.
$\sum_{i \in N} deg (i) = 2∣ R ∣$ La somme des degrés des nœuds d'une graphe est égal au double du nombre d'arêtes dans le graphe.
Si $G$ est un graphe simple, le nombre de parcours de longueur $k$ entre ses nœuds $i$ et $j$ est donné par $(A^{k})_{i, j}$

Graphe Orienté :

Un graphe orienté est un graphe dont les arêtes sont associées à une direction.

Graphe Pondéré :

Un graphe pondéré est un graphe $G = (V, E, w)$ , où $w : E \to R : {u, v} \to w ({u, v})$ est une fonction affectant à chaque arête un poids réel.

Arbre :

Un arbre est un graphe connexe qui ne possède pas de cycle.

Propriétés/Théorèmes : Les Propriétés suivantes sont équivalentes (elles définissent des arbres) :

$G$ est connexe et sans cycle.
$G$ est connexe et $∣ R ∣ = ∣ N ∣ - 1$
$G$ est sans cycle et $∣ R ∣ = ∣ N ∣ - 1$
$G$ est sans cycle et lui ajouter une arête crée un et un seul cycle.
$G$ est connexe et supprimer une arête quelconque le déconnecte.
Deux nœuds distincts de $G$ sont reliés par un et un seul chemin (et $G$ est sans boucle)

Feuille :

Soit $G = (N, R)$ un arbre. On dit qu’un nœud $n \in N$ est une feuille de $G$ si $deg (n) = 1$ .

Propriétés/Théorèmes :

Les extrémités du chemin le plus long dans un arbre sont des feuilles de degré 1. Preuve : Soit $c = (n_{1}, n_{2}, \dots, n_{m})$ un chemin de longueur maximale dans $G$ (ce chemin n’est pas nécessairement unique, mais il en existe au moins un). On voit que $deg (n_{1}) \geq 1$ puisque $n_{1}$ est adjacent à $n_{2}$ . Si $n_{1}$ était de degré strictement supérieur à $1$ , il devrait exister un nœud $n$ adjacent à $n_{1}$ et distinct de $n_{2}$ . Si $n$ se trouve sur le chemin défini plus haut, alors $G$ possède un cycle, ce qui contredit le fait que $G$ est un arbre. Si $n$ ne se trouve pas sur le chemin défini plus haut, alors $c$ peut être étendu en le préfixant par $n$ , ce qui contredit l’hypothèse que $c$ est un chemin de longueur maximale. On en conclut que $deg (n_{1}) = 1$ . Le même raisonnement s’applique à $n_{m}$ , et on a donc identifié deux nœuds de degré $1$ .

Arbre sous-tendant

L’arbre $G^{'} = (N^{'}, R^{'})$ est un arbre sous-tendant le graphe $G = (N, R)$ si $N = N^{'}$ et $R^{'} \subseteq R$

Propriétés/Théorèmes :

$G$ est connexe $\Leftrightarrow G$ possède un arbre sous-tendant

Arbre sous-tendant de poids minimum

$A$ est un arbre sous-tendant de poids minimum de $G$ ssi $A$ sous-tend $G$ et tout arbre $A^{'}$ sous-tendant $G$ est tel que $c (A) \leq c (A^{'})$ .

Exemple(s)

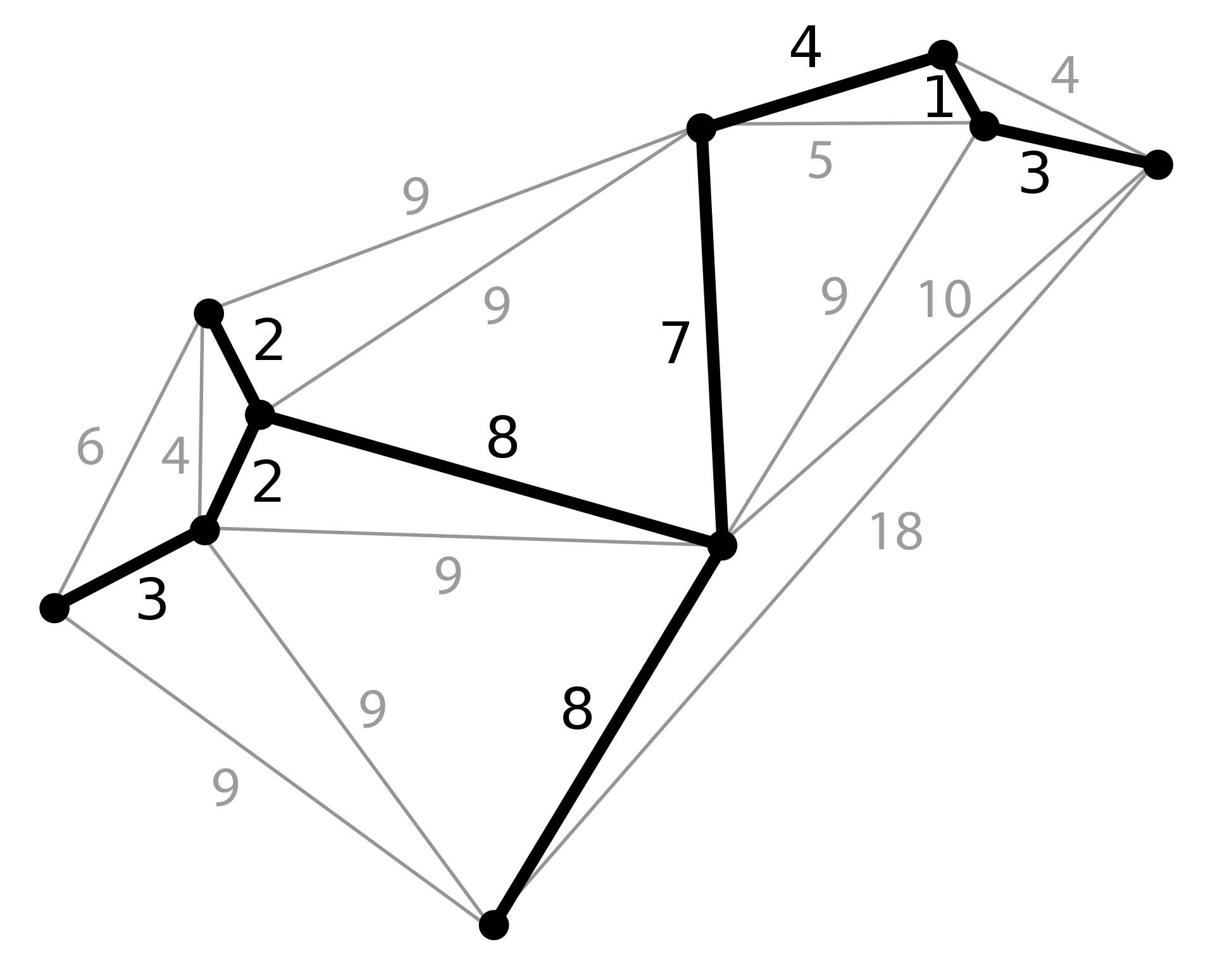
Algorithmes

Cette section reprend les descriptions mathématique, implémentations et preuve d'exactitude de certains des algorithmes les plus importants de la théorie des graphes.

Il est divisé en 4 chapitres :

Algorithme de Bellman-Ford

Maths

In : $G = (N, R)$ un graphe orienté pondéré sans cycle négatif et $s \in N$

Out : Une liste de taille $∣ N ∣$ contenant les distances minimales séparant $s$ de tous les autres nœuds.

Init : $d (s) := 0$ et $d (u) := \infty \forall u \in N - {s}$ . On créé une liste de distances séparant $s$ des autres nœuds. On initialise les distance à une valeur de $\infty$ pour que les comparaisons qui suivent puissent rapidement remplacer cette valeur et la distance séparant $s$ de $s$ est $0$ .

Loop : Répète $∣ N ∣ - 1$ fois :

$\forall (u, v) \in R :$
- si $d (u) + c ((u, v)) < d (v)$ alors $d (v) := d (u) + c ((u, v))$

Description

On créé la liste $d$
Ensuite on répète $∣ N ∣ - 1$ fois la procédure suivante
Pour chaque arête reliant $u$ à $v$ on regarde si la distance à l'arête $v$ peut être raccourcie en prenant la distance à l'arête $u$ plus le poids de l'arête qui les sépare.
$d$ contient les valeurs recherchées.

Implémentation Python

# Cette fonction admet qu'il n'y a pas de cycle négatif dans le graphe. 
def bellman_ford(graph, source):

    distance = {vertex: float('infinity') for vertex in graph}
    distance[source] = 0

    for i in range(len(graph) - 1):
        for u, v, weight in graph.edges():
            if distance[u] + weight < distance[v]:
                distance[v] = distance[u] + weight

    return distance

Complexité

Spatiale : $O (∣ N ∣)$

Temporelle : $O (∣ N ∣ \cdot ∣ R ∣)$

Preuve de validité

Preuve par induction

Observations :

Après $i$ répétitions :

Si $d_{i} (u) \neq = \infty$ , alors $d_{i} (u)$ est le coût d'un chemin de $s$ vers $u$ (pas forcément le plus court)
Si $\exists$ un chemin de $s$ vers $v$ d'au plus $i$ arêtes, alors $d_{i} (v)$ est $\leq$ au coût du plus court chemin de $s$ vers $v$ comptant au plus $i$ arêtes

Si on arrive à démontrer ces observations on aura démontré que l'algorithme est correct.

Cas initial :

On a $d_{0} (s) = 0$ et $d_{0} (u) = \infty \forall u \in N - {s}$

Cas général :

Si $d_{i} (v)$ a été mis à jour selon la formule $d_{i - 1} (u) + c ((u, v))$ alors $d_{i} (v)$ est la longueur du chemin allant de $s$ à $v$ qui suit le chemin allant de $s$ à $u$ et ensuite vers $v$ . Ce qui prouve la première observation.

Pour la seconde observation, si on considère un chemin de longueur minimale $C (i)$ (il peut y en avoir plusieurs) allant de $s$ à $v$ avec au plus $i$ arêtes. Soit $u$ le dernier nœud avant $v$ . Alors, le chemin allant de $s$ à $u$ dans $C (i)$ (qu'on peut noter $Q$ ) est un chemin de longueur minimale avec au plus $i - 1$ arêtes parce que sinon il y aurait un chemin plus court avec au plus $i$ allant de $s$ à $v$ que $C (i)$ ce qui est une contradiction.

Nous faisons maintenant l'hypothèse inductive que $d_{i - 1} (u) = w (Q)$ ( $w$ étant la fonction qui donne la somme des poids des arêtes d'un parcours).

À l'itération $i$ on calcule $d_{i} (v) = min (d_{i - 1} (v), d_{i - 1} (u) + c ((u, v)))$ On sait que $d_{i - 1} (u) + c ((u, v)) = w (Q) + c ((u, v)) = w (P)$ on a donc que $d_{i} (v) \leq w (P)$ ce qui démontre la seconde observation.

Comme il n'y a pas de cycle négatif le chemin le plus court ne passera pas plus d'une fois par chacun des nœuds et donc après $∣ N ∣ - 1$ cycles nous auront toujours le chemin le plus court.

Preuves externes :

MIT
Wikipedia EN, FR

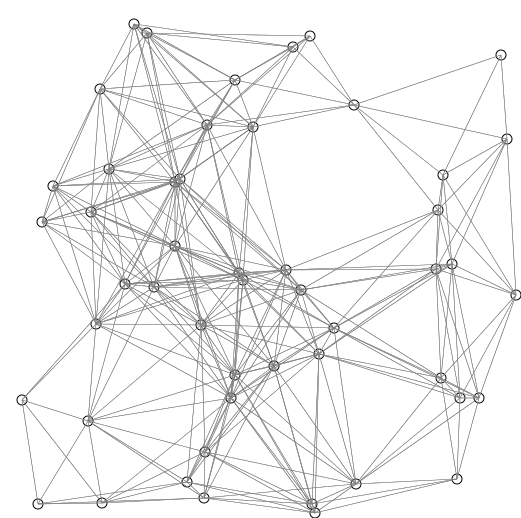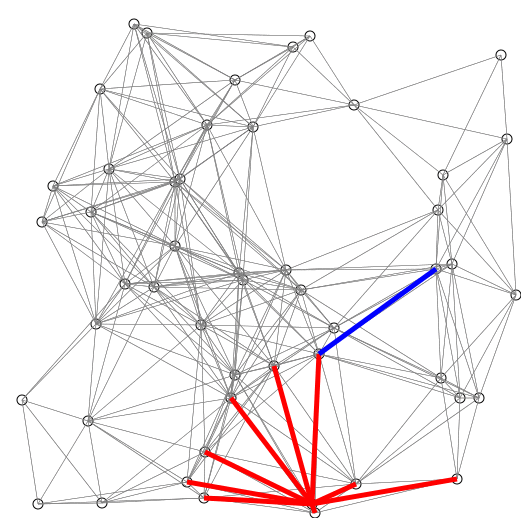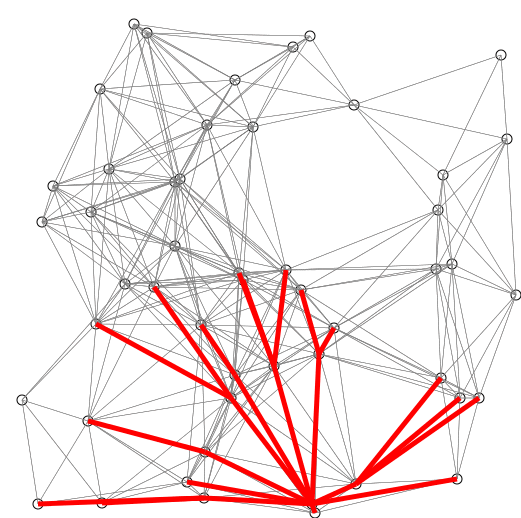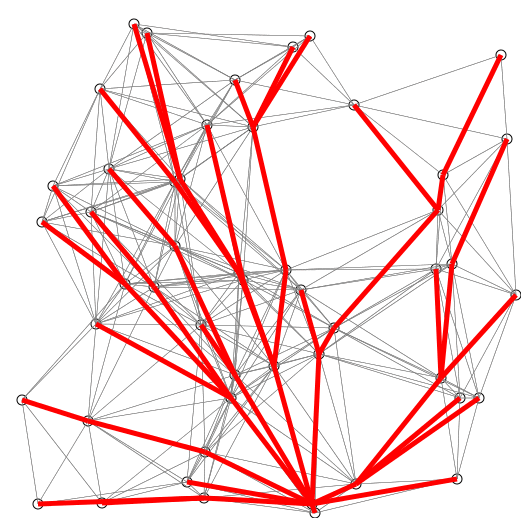
Algorithme de Dijkstra

Maths

In : $G = (N, R)$ un graphe orienté pondéré avec des poids positifs et $s \in N$

Out : Une liste de taille $∣ N ∣$ contenant les distances minimales séparant $s$ de tous les autres nœuds.

Init : Soit $N_{s} := {s}, \overline{N_{s}} := N - N_{s}$ et, $d (u) := c (s, u) \forall u \in N$ ( $d (u) = \infty$ si il n'y a pas d'arête entre $s$ et $u$ ). (où $c (s, u)$ est le poids de l'arête reliant $s$ et $u$ ).

Loop : Tant que $\overline{N_{s}} \neq = \emptyset$ :

$v :=$ un élément de $\overline{N_{s}}$ qui minimise $d (v)$
$N_{s} := N_{s} \cup {v}$ (et $\overline{N_{s}} := N - N_{s}$ )
$\forall i \in \overline{N_{s}} : d (i) := min (d (i), d (v) + c (v, i))$

Description

On créé la liste $d$ de taille $∣ N ∣$ qu'on initialise à 0 pour $d (s)$ , $c (s, u)$ pour les nœuds adjacents à $s$ et $\infty$ pour les autres nœuds. On créé également l'ensemble $N_{s}$ qui contient les nœuds dont on connait la distance minimale ainsi que l'ensemble $\overline{N_{s}}$ qui contient les nœuds restants.
Tant que $\overline{N_{s}}$ n'est pas vide ou tant que $∣ N_{s} ∣ \neq = ∣ N ∣$ on répète la procédure suivante :
On prends l'élément $u$ de $\overline{N_{s}}$ qui est le plus proche de $s$ , on le retire de $\overline{N_{s}}$ et on le place dans $N_{s}$ . Ensuite on regarde pour tous les nœuds restants dans $\overline{N_{s}}$ si la valeur de leur distance dans $d$ peut être raccourcie en prenant $d (u)$ plus le poids associé à l'arête séparant $u$ et le nœud en question
$d$ contient les valeurs recherchées.

Implémentation Python

def dijkstra(graph, source):
    dist = {vertex: float('infinity') for vertex in graph.vertices}
    dist[source] = 0
    
    Q = set(graph.vertices)
    
    while Q:
        u = float('infinity')
	    for vertex in Q:
		    u = min(u, dist(vertex))
        Q.remove(u)
        
        for v, weight in graph.edges.get(u, {}).items():
            if v in Q:
                alt = dist[u] + weight
                if alt < dist[v]:
                    dist[v] = alt
    
    return dist

Complexité

Implémentation naïve :

Spatiale : $O (∣ N ∣)$

Temporelle : $O (∣ N ∣^{2} + ∣ R ∣)$

Meilleure Implémentation

Temporelle : $O (∣ R ∣ + ∣ N ∣ lo g ∣ N ∣)$ Voir : Tas de Fibonacci

Preuve de validité

Todo

Algorithme de Kruskal

Maths/Description

In : $G = (N, R)$ un graphe connexe pondéré

Out : $(N, R^{'})$ un arbre sous-tendant $G$ de poids minimum

Init : On définit $R_{ord}$ l'ensemble trié des arêtes pondérées venant de $R$ ainsi que $R^{'} := \emptyset$

Loop : Tant que $∣ R^{'} ∣ < ∣ N ∣ - 1$ :

$(α, R_{ord}) := R_{ord}$ (on retire la première arête $α$ de l'ensemble trié $R_{ord}$ )
Si $(N, R^{'} \cup {α})$ est sans cycle, alors $R^{'} := R^{'} \cup {α}$ (une condition équivalente est : Si l'arête relie 2 arbres distincts alors...)

Implémentation Python

# Cette fonction admet l'existance de certaines 
# méthodes et classes qui permettent de rendre
# le code plus lisible.
def kruskal(graph, rPrime):
    graph.sortByWeight()

    for edge in graph.edges():
        weight, u, v = edge
        if hasCycle(rPrime.union(edge)) == false:
            rPrime = rPrime.union(edge)

    return rPrime

Complexité

Spatiale : $O (∣ N ∣ + ∣ V ∣)$

Temporelle : dépend surtout de l'algorithme de triage mais dans le meilleur des cas : $O (∣ R ∣ lo g ∣ R ∣) = O (∣ R ∣ lo g ∣ E ∣)$

Preuve de validité

Todo

Théorie des Graphes

1. LEPL1108 cours donné à l'UCLouvain