Théorie des Graphes

Matrice d'incidence :

La matrice d’incidence d’un graphe $G=(n,R)$ est la matrice de genre $|N|\times |R|$ dont chaque entrée $(i,\alpha )\in N\times R$ vaut :

• $2$ si l’arête $\alpha$ est une boucle sur le nœud $i$,
• $1$ si $\alpha$ relie $i$ à un autre nœud,
• $0$ si $\alpha$ n’est pas incidente à i.

Exemple(s) :

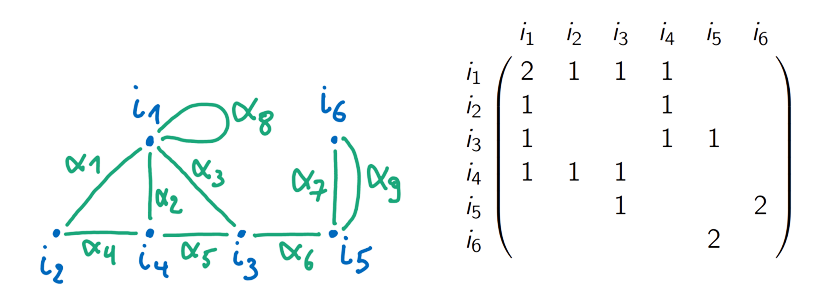
Matrice d'Adjacence :

La matrice d’adjacence $A$ est de genre $|N|\times |N|$ :

• $a_{i,j}:=$ nombre d’arêtes reliant $i$ et $j$ si $i\ne j$
• $a_{i,i}:=$ deux fois le nombre de boucles sur $i$

Exemple(s) :

Propriétés/Théorèmes :

1. Soient 2 graphes $G_1$ et $G_2$ avec comme matrices d'adjacence $A_1$ et $A_2$. $G_1$ et $G_2$ sont isomorphes si et seulement si il existe une matrice de permutation $P$ tel que : $$P{A}_1{P}^{-1}=A_2$$ $A_1$ et $A_2$ sont donc semblables. Dit autrement: si on peut permuter les noms des nœuds de telle sorte que que $G_1$ devient $G_2$ alors les graphes sont isomorphes et la permutation des noms est équivalent à permuter les lignes et les colonnes de la matrice ce qui correspond à la formule ci-dessus.
2. ${\sum }_{j\in N}{a}_{i,j}={\sum }_{j\in N}{a}_{j,i}=\text{deg}(i)$ La somme des termes sur une lignes ou une colonne correspond au degré du nœud associé à cette ligne/colonne.
3. ${\sum }_{(i,j)\in N^2}{a}_{i,j}=2|R|$ La somme de tous les éléments de la matrice est égal au double du nombre d'arêtes dans le graphe.
4. ${\sum }_{i\in N}\text{deg}(i)=2|R|$ La somme des degrés des nœuds d'une graphe est égal au double du nombre d'arêtes dans le graphe.
5. Si $G$ est un graphe simple, le nombre de parcours de longueur $k$ entre ses nœuds $i$ et $j$ est donné par $(A^k{)}_{i,j}$